
Is there an Order in the Chaos of Primes?
Prime Numbers, Conjectures, Reimann Hypothesis
Pulkit Jindal and Archita Banka
Primes.. Something we’ve known about nearly as long as we remember, numbers with no divisors other than themselves and 1. However they are one of the greatest mysteries of mathematics despite being so simple and common- place. What is it that makes them so mysterious?
Well many things but most importantly the mystery behind their distribution. They appear to be distributed essentially randomly over the number line.
On average they decrease in number meaning among large numbers, primes are more sparse in nature. This leads to the natural question, is there a largest prime number? If yes, then what is it?
Is it 393,050,634,124,102,232,869,567,034,555,427,371,542,904,833? Mmm no.
Although many things about primes are unknown, this is surprisingly simple to disprove.
If we had primes \[p_1,p_2, \cdots ,p_k\] with \(p_k\) being the largest then the number \( (p_1 \cdot p_2 \cdot p_3 \cdot \dots \cdot p_k) + 1\) would be not divisible by any of these primes implying that either it is prime or some other prime larger than pk divides it. This leads to a contradiction that \(p_1 \cdots p_k\) were all the primes, proving that there are infinite primes.
How are the primes distributed if there are infinite of them?
A famous conjecture related to this is the Twin Prime conjecture which states that there are infinite pairs of primes that differ by 2, for example 5, 7 or 11, 13. This seems to contradict what was stated earlier that primes get more sparse, but even if they are less dense for larger numbers but may still differ by 2.
This conjecture though looks simple is still unproven. A lot of work has been done on this area and many lower bounds for infinite pairs of primes differing by some value k have been studied upon. The maths behind those is quite difficult and will be omitted here but one of the lowest bounds obtained until now is 246.
Another famous unsolved problem about primes is Goldbach’s Conjecture, proposed in 1742. It states that every even integer greater than 2 can be expressed as the sum of two prime numbers.
For example, \(10=3+7, 18=5+13, 28=11+17\).
This has been checked by computers for even numbers up to extremely large values (currently beyond \(4×10^{18}\)), and no counterexample has been found. Despite this, a proof still eludes mathematicians. The conjecture captures the idea that although primes get sparser, they are still “numerous enough” to combine in structured ways. Like the twin prime conjecture, proving it would give us a much deeper understanding of prime distribution.
Both the Twin Prime Conjecture and Goldbach’s Conjecture highlight how little we truly know about the structure of primes, but is it really that significant when all such results seem unproved? Let’s see a result that shows a structure in the distribution of primes.
A result on primes that is not unproven –
The Green–Tao Theorem
A landmark result about primes that came in 2004, when Ben Green and Terence Tao proved that the prime numbers contain arbitrarily long arithmetic progressions. This means there exist sequences of primes like \(p, p+d, p+2d,\cdots, p+kd\) for any length k, where each term is prime.
For example, \(5, 11, 17, 23, 29\) is a progression of five primes equally spaced apart. Before this theorem, it was not even clear that progressions of any arbitrary length existed among primes. This result showed that primes, although seemingly random, possess surprising large-scale structure.
So instead of tackling problems related to distribution of primes one by one, mathematicians turned to deeper tools that would help capture the global behaviour of primes — most famously, the Riemann Zeta function, where the heart of research on primes and the most important tool in finding primes lies.
Before we introduce the Riemann Zeta function let us start with a few common results.
Let’s start with harmonic sum,
\[ \sum_{n=1}^{\infty} \frac{1}{n} \]
which diverges meaning that the sum tends to infinity when calculated over infinite terms.
Interestingly, if we all the individual terms were squared and then evaluated, the summation it turns out that the sum actually converges.
\[ \sum_{n=1}^{\infty} \frac{1}{n^2} = \frac{\pi^2}{6}. \]
But why in the first place did we introduce such a random function? Because this function is actually the basis of the Riemann Zeta function.
We define the Zeta function as :
\[\zeta(s) = \sum_{n=1}^{\infty} \frac{1}{n^s}, \quad \Re(s) > 1.\]
Now, a very first natural question to ask is how is this function even connected to primes? On first glance it seems to be completely random, but if we recall,
each number has a unique prime factorization we realize that this function can be rewritten as :
\[\zeta(s) = \prod_{p \ \text{prime}} \frac{1}{1 – p^{-s}} \]
and further simplified to show a deep connection between primes and \(\zeta(s)\).
Even after all this, it’s a simple function and is insufficient to lead us to the distribution of primes. However if we extend the function to the complex plane we realize that the function begins to become interesting.
But there’s still a problem: the original function diverges for values less than 1 and that still holds here — for values with a real part less than 1, the function diverges and thus our graph is only half filled.
However using some complex analysis techniques this graph can be extended to fill in the remaining portion and this final graph is referred to as the Riemann Zeta function.
Giving a beautiful graph consisting of multiple spirals and also one of the holy grails of mathematics.
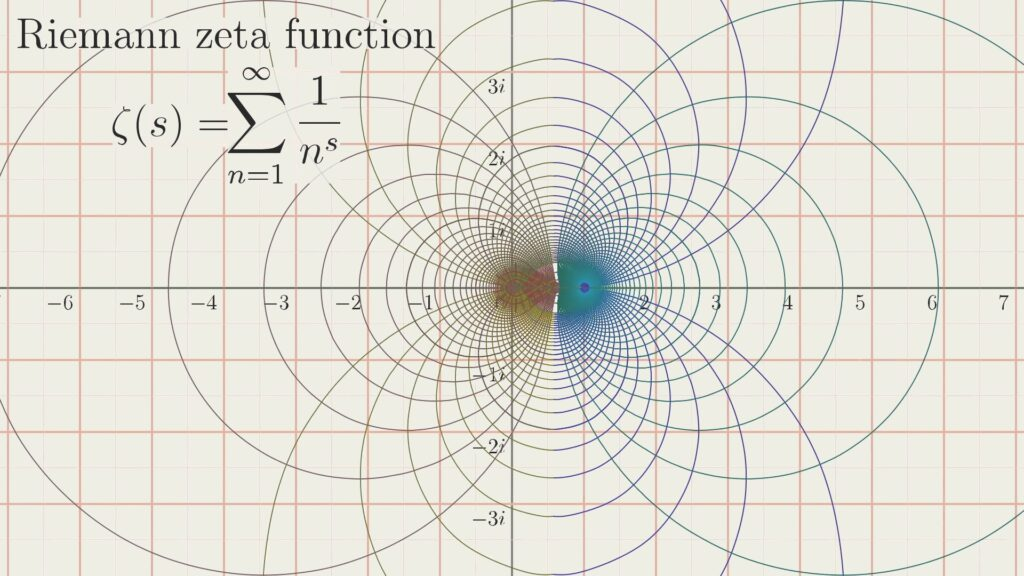
Ok, but what now?
Even after we’ve done all this it still seems far-fetched to think this could connect to the original question. Riemann first proved that non-trivial zeroes of the Riemann Zeta function have real values lying between 0 and 1.
Non-trivial zeroes here refers to values which make the Riemann Zeta function equal to 0 and are not trivial meaning they aren’t even negative integers.
He hypothesized that all these zeroes actually have real part equal to one-half.
This hypothesis remains unproved and is one of the millennium problems. More about the millennium problems will be linked below.
Now we can connect this to primes. Instead of counting primes directly, we define the Chebyshev function as follows:
\[\psi(x) = \sum_{p^k \leq x} \log p,\]
where the sum is taken over all prime powers \(p^k \leq x\). This means that the function increases by \(\log p\) at each prime \(p\), by \(\log p\) again at \(p^2\), by \(\log p\) again at \(p^3\), and so on.
If we take a straight line (the approximation \(\tfrac{x}{\ln x}\)) and then to that function, we add waves with frequency corresponding to the Riemann Zeta zeroes then we will obtain a curve that matches exactly with this function.
Thus we will have obtained the distribution of the primes and how a long winding tail of various results can finally lead us back to the mysteries of primes.
All that remains is for the Riemann Hypothesis to be proved.
References used for this article:
https://www.youtube.com/watch?v=zlm1aajH6gYt=324s
The book Primes Obsession by John Derbyshire
Links and helpful resources :
For analytic continuation: https://www.youtube.com/watch?v=sD0NjbwqlYwt=42s
An interesting read could be The Music of the Primes by Marcus du Satoy
