Group Theory and Modern Encryption

Group Theory, Cryptography

Swaminath Shiju

Put yourself in the shoes of a British cryptographer during the second installment of the war to end all wars, working to crack the Germans’ encrypted messages. The chief object of your nightmares is the German enigma machine. A marvel of German engineering, it was an electro-mechanical box used to encrypt confidential command and diplomatic communication.

How does it work? Crudely speaking it is simply a glorified typewriter. When we press a key say “A” current flows from key to the plug board where you can use external wires to connect letters, say “A” is connected to “M” then the current flows as though “M” was pressed to the next part of the machine. This part consists of three rotors, each of which have internal connections that uniquely scramble the letters. After traversing all three rotors, the current reaches a reflector, then passes back through the rotors in reverse and finally the plug board again—lighting up a letter, say “G”. That’s your encrypted output. Crucially, after each key press, the rotors rotate, changing the configuration.

The Engima also was very conveniently reversible. It was in fact self-inverting. That is in the previous example with the same initial configuration if I press “G”, “A” would light up. So reversing a message needs the exact initial condition.

Now here is the thing 3 spinning rotors chosen from 5 possible rotors, each having 26 possible initial positions, and 10 plug board wires – there are 158,962,555,217,826,360,000 possible initial configuration. Each giving a different encryption of the message and the only way to decrypt is by knowing the initial configuration. The naive approach to crack the message is simply brute-force the initial configuration, decrypt the encoded message and see if the output looks like its a message and not gibberish.

With the naive approach and 1940s computing power you’d be lucky to decrypt a weather report before the end of the war. How would we even start analyzing a problem like Engima?

Meet, in my opinion one of the most elegantly simple and powerful concept in higher mathematics – Group Theory

What even is a Group?

Imagine a square with vertices numbered from 1 to 4. It is somewhat less glamorous than the elusive Enigma but stick with me here. Think of how many ways we can rotate and flip this square.

Notice how many different ways of composing together transformations gives the same final configuration. I want to denote rotation by $x^\circ$ as $R_x$ and $H$ for the horizontal flip.

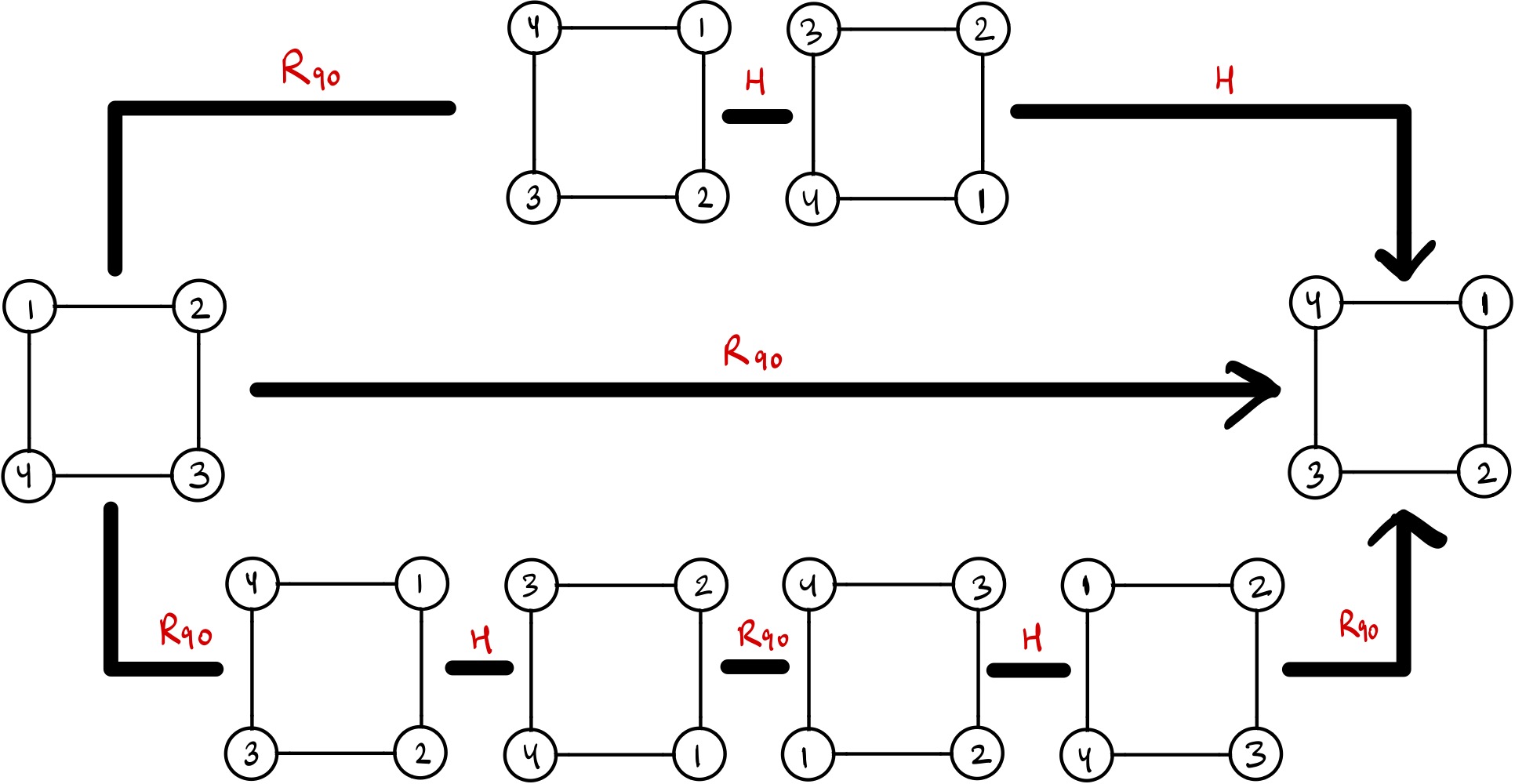
So the pictures I can concisely write as

\[ R_{90}HR_{180}H=R_{270}=R_{90}HR_{90}HR_{90} \]

I’ve written them in a way that looks like “multiplication”. Take for example – $R_{90}H$: This represents the state of the square after applying $H$ and then $R_{90}$.

A nice fact you can see is that you can think of $xyz$ as either $x(yz)$ or $(xy)z$ and it would give the same final state. You can use the above examples to sanity check that this is in fact true. To someone with a little mathematical background this property is called Associativity.

Now if we write down all possible orientations of this square we can represent them with simply the notation we already introduced

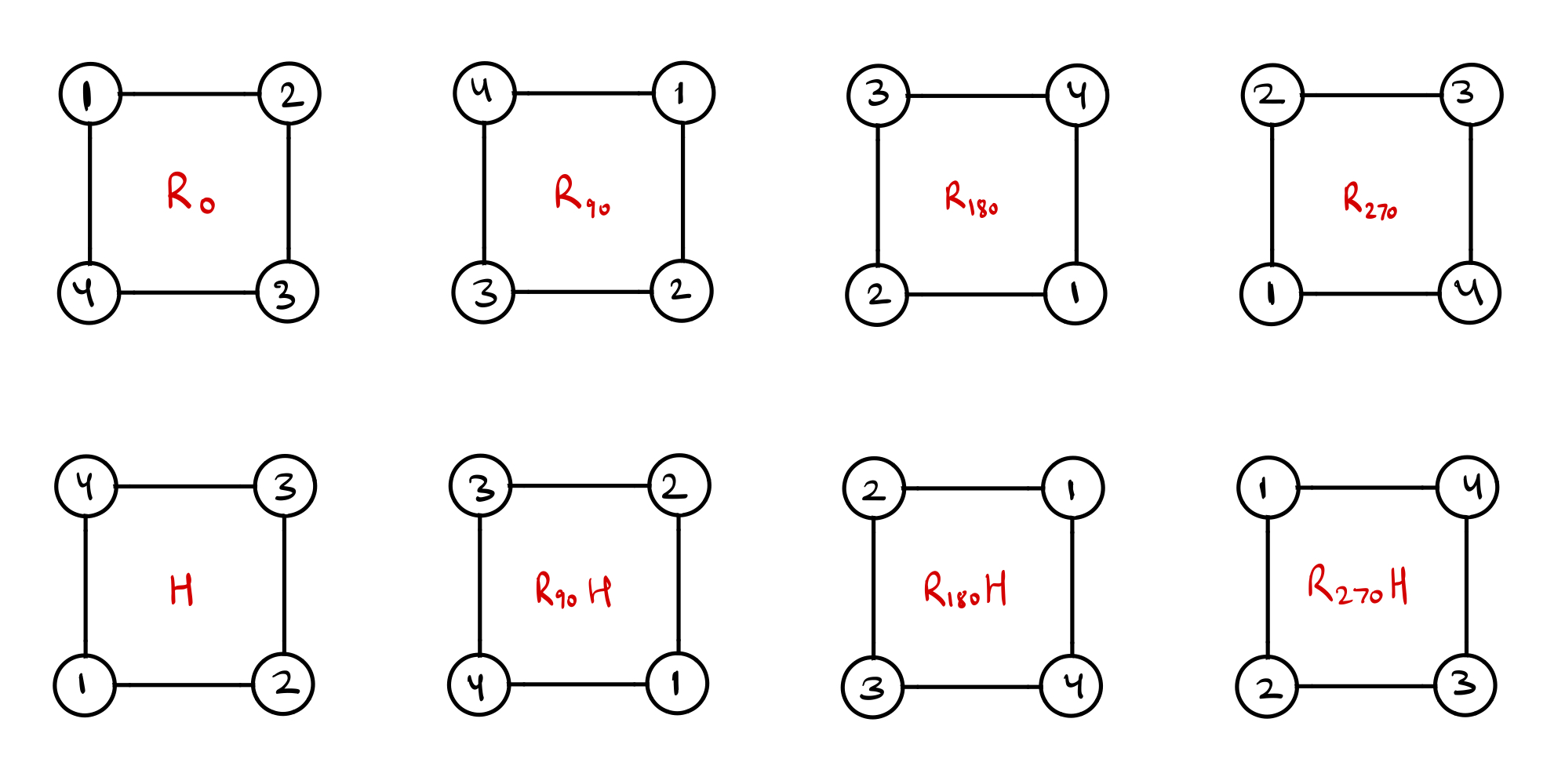
Now how is this somewhat strange thought experiment related to the mysterious notion of a group. The set we enumerated above – the set of all possible configurations of out imaginary square is a … Group.

Now what is a group? A group is a set of some objects we can define a binary operation on (i.e take 2 objects do something with them and create another object). This operation needs to satisfy some nice properties.

What Makes a Group?

Let $G$ denote our group set, and $x,y,z\in G$ are elements in the group, $xy$ is the binary operation on $x$ and $y$.

Associativity: The property we discussed before – $(xy)z = x(yz)$ so we can unambiguously define $xyz$.
Closure: Operating with any 2 elements in the group will give another element in the group – $xy\in G$
Identity: There exists some $e\in G$ such that $ex=xe=x$ called the identity element.
Inverse: For each $x\in G$ there exists some $x^{-1}\in G$ such that $xx^{-1}=x^{-1}x=e$

⁠Note: Commutativity i.e $xy=yx$ is not a required property. See $x=H, y=R_{90}$

⁠Removing the square itself and looking it as simply a list of numbers you can notice it is just in some sense constrained permutations. Which were incidentally the earliest types of groups studied and more general groups can still be a seen as a more abstract permutation.

Another simple group you can play around with is $Z_{n}$ the group of all non-negative integers less than $n$ the operation being addition modulo $n$.

This is shockingly all the basics you need for Group theory to keep up with the following conversation.

What does this have do with Enigma?

Back to our machine. We saw how permutations and groups have an intimate relation. Now instead of a square or numbers consider letters.

Every key press effectively applies a joint permutation that looks like:

Plug board: a permutation $P$
Rotors: $A_1, A_2, A_3$
Reflector: $U$

So the full encryption becomes: \[PA_1A_2A_3UA_3^{-1}A_2^{-1}A_1^{-1}P^{-1}\]

This captures the forward and reverse traversal.

After each key-press the rotors turn too.

\[A_i^\prime =\rho A_i \rho^{-1}\]

Where $\rho$ is the cyclic permutation that take A to B, B to C and so on. So when it acts on another permutation it does the same thing as rotation.

That extra $\rho^{-1}$ comes from the fact that when the rotors spin only the input disc changes but outputs remain physically static.

Now that we have fully group-theoretic representation of the device is there some nice elegant way to break it?

Breaking Enigma

Enigma was incredibly good at what it did. The cipher operators … well not as much. It is likely that properly enforced good operating procedures would’ve made the Enigma unbreakable to the technology of the time. However bad operating practices did eventually cause its downfall. Without getting too much in WW2’s military history, in a nutshell the issue was crucial parts of the message being predictable. Like say a common header.

Contrary to popular belief my man ~~Benedict Cumberbatch~~ Alan Turing was not the first person to break Enigma. In the early 1930s, Marian Rejewski, a young Polish mathematician, was the first to make real progress. He modeled the Enigma machine using permutation groups, leveraging deep results from group theory—particularly the theory of cycles in permutations. Cycles here were important since the plug board crucially can’t effect length and number of cycles in the output.

Rejewski broke an older version of the Enigma machine with only $3$ rotors giving 6 different rotor positions. He did so remarkably by deducing the internal structure and wiring from the intercepted messages alone. The enigma machine was then changed several times to improve its security among which one for picking $3$ rotors from a total $5$ making Rejewski’s method unfeasible. Alan Turing and the team at Bletchley Park then modified a device made by Rejewski known as the Bombe to work with the newer enigma machine and succeeded in breaking it.

Enigma is still however a centuries old encryption technique, it likely wouldn’t stand up to today’s standards – if sufficiently motivated any modest server farm could crack even a perfectly operated Enigma.

So what does encryption look like in the modern age (Spoilers – Its still carried by Group Theory). We’ll look at 2 of them and how a single question makes them both secure.

The Discrete Logarithm Problem

Suppose we have the equation \[2^x=12\] in reals. This is easily solvable using the logarithm function \[x=\frac{\log 12}{\log 2}\] however this equation could also make sense in the context of say modular 13 arithmetic. \[2^x\equiv 12\bmod(13)\] One solution is \[x=6\]
The group we worked with just now is the group of integers less than $n$ with the operation as multiplication modulo $n$.

Note: All non-negative integers less than $n$ are not elements of the above mentioned group only co-primes are – Can you think of why that is so? (Write it down and think of how we would implement inverse)

In the case of general groups there is no efficient way to solve this problem. Since we only worked with a small group (The above group has only 13 elements in fact) we could easily just brute-force the solution. For larger general groups to the best of our knowledge there is no polynomial time algorithm to find discrete logarithm (discrete since we working in the context of finite groups and logarithm since we reversing “exponentiation”).
One of the best algorithms we have today is called the baby-step giant-step algorithm whose time complexity is still exponential in size of input in bits (It is however $O(\sqrt{N})$ where N is group size – size of input is roughly exponential of group size).

From an information theory stand-point you can see how it is true, if $b$ is number of bits then \[b\approx O(\log_2 N) \implies N \approx O(2^b)\] and substituting in the complexity equation we end up with a roughly exponential time.

Is the problem always hard?

Matter of fact no its not. Lets consider the group of all non-negative integers less than $p$ where $p$ is prime with the operation addition modulo $p$. Notice how exponentiation of the group operator translates to what we would commonly consider as repeated addition.

So our problem now is, find k given

\[k\circ a = b \quad a,b \in G\]

It is very important to note $k$ need not be an element in the group – here I’ve specifically used $\circ$ to denote repeated addition and not the group operation.

If we now remove ourselves from group theory and look at this as a simple problem in number theory – so we can utilize tools from there with now gives us access to two operators the group operator addition and another operator multiplication. The above problem translates to solving the below diophantine equation with variables $(k,m)$

\[ak + pm = b\]

of course solution only exists iff $\gcd(a, p) \mid b$ but since $\gcd(a, p)=1$ there always exists a solution. Now we can use the ridiculously efficient extended Euclid’s gcd algorithm as usual for linear diophantine equations to solutions for $(k,m)$.

But when is it hard?

The group we took above the group of integers under addition in modulo is an extremely simple group (One in fact so well studied an entire branch of mathematics is built upon it).

This made it possible to have a very fast algorithm that solves DLP in that group. I used specific results in number theorem solely for convenience. That is precisely why I said solving DLP is to the best of our knowledge very hard to solve – It is infact an open problem to find whether an efficient algorithm for DLP can exist. Maybe a couple genius ideas could entirely break it, though unlikely it is possible since we haven’t proven otherwise.

Lets look at a toy cryptographic problem statement to meet our first use of DLP. Say you were the owner of a server that a lot of people send private messages to. Can you devise a cryptographic algorithm such that everyone can send you encrypted messages but only you can decrypt every message.

Welcome RSA

This is a problem that can be solved using what I will refer to as the public key encryption, the most influential of which was the RSA cryptosystem. I will first give a brief overview of the protocol and how it works before explaining why its secure.

Initialization

Generate 2 large (really large like 512 bits large) primes numbers $p,q$
Multiply them together to get $N=pq$
Take some number $e$ such that $\gcd(e, \phi(N))=1$
Find $d$ such that $ed\equiv 1 \bmod(\phi(N))$

$\phi$ is the Euler totient function

Here $(e, N)$ is your public key. i.e everyone know it and people can use it to encrypt their own messages. While only you, with access to $d$ the private key can decrypt them.

A key requirement of any public key cryptography system is to ensure there is no feasible way to derive the private key from the public key.

Encryption

Say you have some message, first convert it into an integer $M$ using some form of encoding
Compute $C=M^e\bmod(N)$
C is your encrypted message, you can broadcast $C$ and only the intended recipient can decrypt it.

Decryption

You have $C$, compute $C^d\bmod(N)$
From our derivation of $C, d$ \[C^d\equiv \left(M^e\right)^d \equiv M^{ed} \equiv M^{k\phi(N)+1}\equiv M \bmod(N) \]

How is it secure? Say you were a malicious attacker determined to find the private key. How would you do that? The only possible way is to send a message yourself so then you know $M, C, e, N$ how to compute $d$ from this?

We know \[ed\equiv 1 \bmod(\phi(N))\]
but $\phi(N)=(p-1)(q-1)$. Factoring large numbers is also an extremely hard problem. Similar to DLP it is also exponential in time complexity. So, since $\phi$ needs you to find $p,q$ by factorizing $N$ this method is not feasible.

We also know
\[C^d\equiv M \bmod(N)\]
This is simply the discrete logarithm problem which we previously discussed and is not feasible to solve.

When there are mathematical processes like these (DLP and Integer factorisation) of the class NP (polynomial time to check if a given answer is correct but exponential to find an answer) there is almost always scope to create a cryptographic algorithm from this.

What about other groups?

Another group I want to talk about has a definition that’s rather more visual than the ones we discussed so far.

Say hello to the group generated by an elliptic curve. An elliptic curve is simply a plane curve described using \[y^3=x^2+ax+b\]
How on earth would this describe a group?

Consider two points on this curve $P,Q$ we can describe a third point on the curve $R$ as follows. Draw line through $P,Q$ which intersects the curve again at some point $R$. The mirror of this point in the x-axis is $R^\prime$.

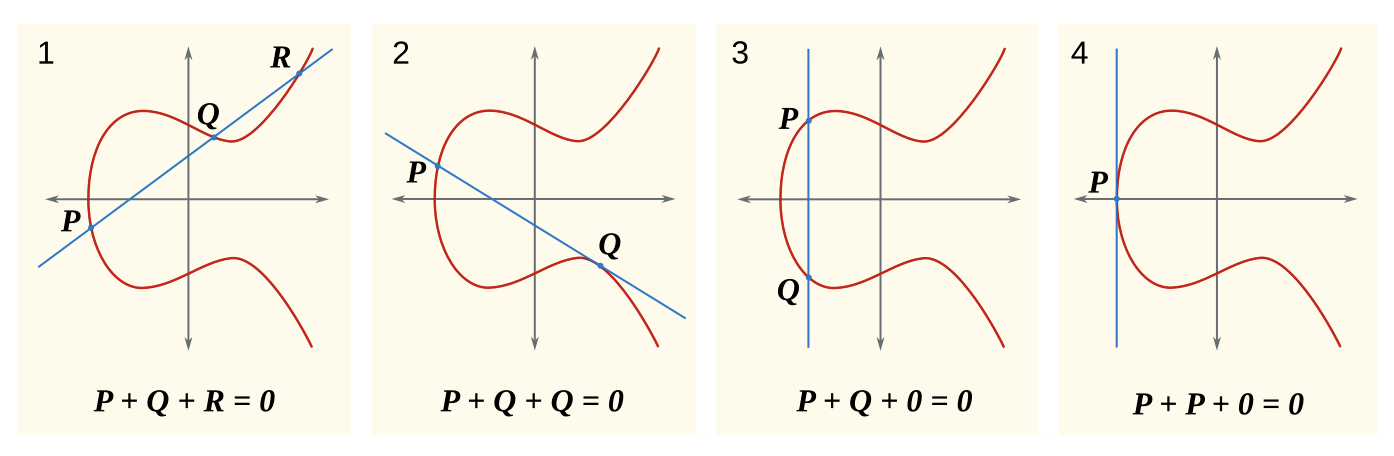
$0$ is the point at infinity – it is a concept in geometry added for convenience for describing the intersection of parallel lines

This is clearly a binary operation of points on the curve to give another point on the curve.

The set of all points that lie on the curve together with “the point at infinity” forms the group generated by the elliptic curve.

A fact mathematicians found that makes this group useful is that we can consider the curve generated by the equation on integers modulo $p$ instead of the reals to construct a group with complex structure.

Now why do we need a new group? RSA already works nicely.

One of the drawbacks of RSA is the key-size. Key size and security will always be a trade-off. Standard RSA recommends 512 bits or more but security of that is also called into question now using dedicated hardware (Though expensive and power hungry).

Elliptic curve cryptography also uses the same fact about solving DLP being incredibly hard but since its structure is more complicated than simple integers it can achieve security comparable to RSA with significantly smaller key sizes.

Conclusion

Group theory ( and related fields xD ) play a central role in modern cryptography, from understanding the Enigma machine’s complex inner workings to ensuring the security of algorithms like RSA and elliptic curve cryptography.

By studying groups and their operations, we can model encryption processes and recognize the mathematical problems, like DLP, that make encryption secure. As cryptography advances, these mathematical foundations continue to ensure privacy in our increasingly digital world.

[On the concept of group:] … what a wealth, what a grandeur of thought may spring from what slight beginnings.

~ Henry Baker