Untangling Knots: AI Reveals Hidden Connections in Topology

In 2021, researchers from DeepMind and the University of Oxford demonstrated that AI is more than just calculation — it can discover. Their work focused on knot theory, the study of how loops can twist and tangle in space, and how such knots can be distinguished using mathematical quantities known as invariants.

For decades, mathematicians suspected a hidden link between two kinds of invariants — one based on a knot’s geometry, the other on its algebraic structure — but no one could pin it down. DeepMind’s team trained an ML model to discover such a pattern and surprisingly, this revealed that a particular algebraic quantity — the signature — was directly related to the geometry of the knot, which was not previously known or suggested by existing theory.

Attribution techniques from machine learning guided Professor Lackenby to discover a new quantity, the natural slope, that hints at an important aspect of structure overlooked until now. Together they were then able to prove the exact nature of the relationship, establishing some of the first connections between these different branches of mathematics.

This wasn’t a proof — it was a conjecture born from pattern recognition at a scale beyond human intuition. Guided by the AI’s insight, mathematicians later proved the relationship, turning the AI’s hunch into a brand-new theorem in knot theory.

The Counterexample Hunter: AI Plays to Win in Combinatorics

Another novel application of AI in mathematical discovery involves reframing abstract problems as competitive games. Researcher Adam Wagner successfully applied this technique, using Reinforcement Learning (RL) to solve several open problems in combinatorics and graph theory.

Disproving a mathematical conjecture often requires finding a single counterexample. Searching for that counter example is like finding a needle in an infinite haystack. Wagner’s insight was to transform this search into a game that an RL agent could learn to master. He framed combinatorial conjectures as graph-building games where the RL agent incrementally constructs graphs and is rewarded for breaking conjectured bounds. Using a simple neural network trained with a cross-entropy–style method, the system generates many candidate graphs, learns from the best counterexamples, and improves over time. By changing only the reward function, the same framework can be applied to many different problems in graph theory and combinatorics.

Despite its simplicity, the approach produced real results. The RL agent found counterexamples to several open conjectures and, in later reimplementations, helped disprove dozens of proposed spectral bounds. Even when it couldn’t solve problems outright, it often guided human mathematicians toward solutions. By gamifying the search, a directionless human exploration is transformed into a directed, reward-driven optimization process that is perfectly suited to the strengths of modern RL algorithms.

Automated proof generation and verification

Imagine a world where every mathematical proof is perfectly, unbreakably true because a computer has verified every single logical step. This is the promise of formal mathematics, often called the “grammar of truth”. The only problem… Translating a brilliant, intuitive human idea into this ultra-precise computer language has always been a painstakingly slow and difficult process. It’s a major bottleneck in mathematical progress.

Enter a new generation of AI-powered assistants like LeanDojo and LeanCopilot. These aren’t your old symbolic solvers that just crunch numbers; they are sophisticated partners in the act of proving.

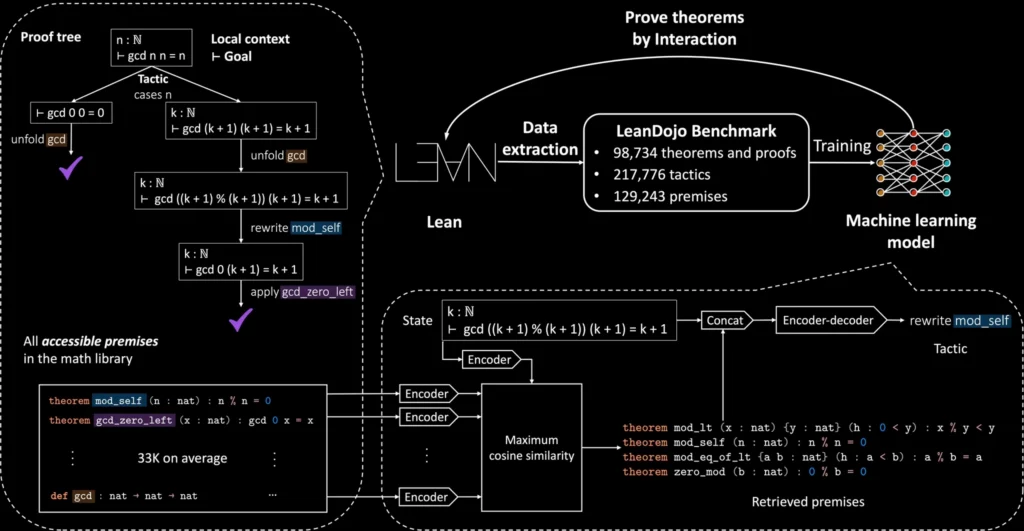
How it Works? Learning to Reason: Built upon powerful theorem-proving platforms like Lean 4, these tools use LLMs that have been trained on thousands of existing formal proofs. By analyzing this vast library of human knowledge, they learn the very patterns of mathematical reasoning.

Their capabilities are transformative:

• Suggesting the Next Step: When a mathematician gets stuck, the AI can suggest missing logical links or intermediate steps (lemmas) to advance the proof.
• Repairing Broken Proofs: If a line of reasoning fails, the AI can analyze the error and attempt to repair the proof automatically.
• Automating the Tedious: They can fill in the logical gaps, handling the meticulous but uncreative parts of a proof, freeing up human intellect for bigger challenges.

In tests conducted by Princeton researchers, LeanDojo was able to successfully complete up to 50% of the unfinished proofs it was given—a monumental leap in automating formal verification.

In this process, humans provide the creative spark, the deep intuition, and the strategy for a proof while AI acts as a tireless, logical assistant, ensuring that every detail is correct and converting human insight into formally verified truth. In this new partnership, machines handle the rigorous verification of our logic, empowering humans to push the boundaries of what logic itself can achieve.